【学习记录】深度学习基本概念

• 前言
• 一个简单的例子理解机器学习的过程
• 学习算法的几个基本概念
  • 回归问题与分类问题
  • 有监督学习与无监督学习
  • 一种重要的模型——神经网络
    • 线性方程组
    • 非线性的激活函数
      • 多层网络的意义
      • 非线性分类更贴近实际
      • 概率
  • 评价神经网络的效果
    • 损失函数
    • 二次损失函数 quadratic loss
    • 梯度下降算法
      • 梯度
      • 梯度下降算法
    • 参数 (parameter) 与超参数(hyper parameter)
      • 超参数 alpha– 学习速率
• 思考题

前言

这是一份我的学习记录，本文知识点来源于【实验楼】网站的课程使用 Python 实现深度神经网络，在此整理笔记。

一个简单的例子理解机器学习的过程

• 计算圆的面积

# 代码片段 2
def learn(model,data):

    ... # 通过数据data训练模型model的代码

    return model # 已经训练好参数的模型

def test(model,x):

    ... # 将x输入模型model中得出结果y的代码

    return y # 返回计算结果--圆的面积

trained_model=learn(init_model,data) # 通过训练得到模型trained_model
y=test(trained_model,x=100) # 得到半径为100的圆的面积

简单解释

• learn() 函数的具体实现暂且不提， 它的作用是，会使用通过数据 data 训练模型 model ，当我们需要计算一个新的圆的面积时，就调用 test 函数，根据训练好的模型去计算其面积。
• 这里先把 learn() 视作黑盒子，我们不需要事先知道输入和输出之间的关系，也不需要手动设置任何参数，只要把数据 “喂给” 学习算法 learn , 它就会自动得出一个能够解决问题的模型。
• 在训练过程中，模型 model 其实是 “学习” 到了输入和输出之前的关系以及相关的参数。就像是一个数学家通过对圆的观察，得出了圆的面积和半径的关系，并且求出了圆周率

这就引出机器学习的基本部分

• 用来解决问题的模型model
• 学习数据（或者说训练数据）data
• 让模型model通过数据data学会解决特定问题的学习算法learn
• 用来纠正模型的test方法

学习算法的几个基本概念

回归问题与分类问题

• 回归(regression): 例如机器学会计算圆形面积的例子属于回归问题。即我们的目的是对于一个输入 x，预测其输出值 y，且这个 y 值是根据 x 连续变化的值。
• 分类(classification): 事先给定若干个类别，对于一个输入 x，判断其属于哪个类别，即输出一般是离散的。比如图片英文字母识别。

有监督学习与无监督学习

• 有监督学习，即在训练过程中，输入x得出y，而这个y的正确答案也事先准备好，用来纠正模型。
• 无监督学习，没有事先准备正确答案，一般用于聚类(cluster)问题，即给定一批数据，根据这批数据的特点，将其分为多个类别，虽然我并不知道这每个类别所代表的具体含义。
  • 这一点特别有趣，可以从大数据中发现人直觉难以察觉的信息，当中可能蕴含极大价值。
  • 比如网络商城的商品推荐算法可能会根据用户的使用习惯，以往的浏览历史等，将用户分为多个类别，同一类别的用户在行为模式上可能比较相似。而事先并不知道最终会划分出多少个类别，每个类别有哪些共同特点。

一种重要的模型——神经网络

线性方程组

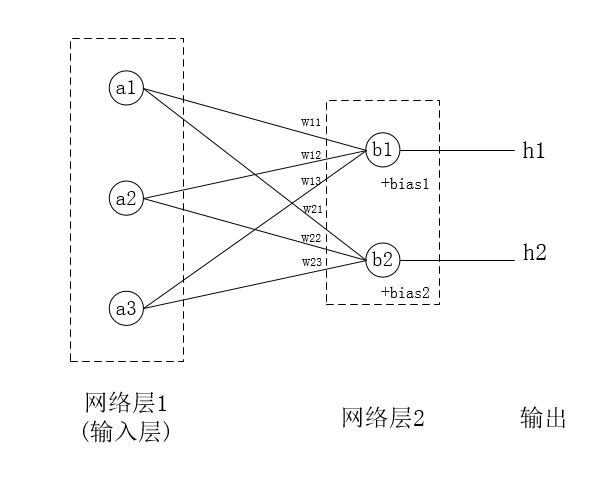
简单解释

上图中网络层１与网络层２的节点，称作神经元，a与b的连接，有笛卡尓积（直积）的条数，即〈x，y〉(x∈a，y∈b)的a×b的交集。它们的连接的数学关系，如下

a1*w11 + a2*w12 + a3*w13 + bias1 = b1
a1*w21 + a2*w22 + a3*w23 + bias2 = b2

这是一个线性方程组

• a, b 神经元，从数学上看，是一个值
• w 权重
• bias 偏移量

写成矩阵的形式：

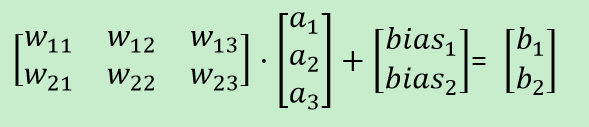
对于网络层2中的神经元b，它的值在传给输出之前, 会先经过一次非线性运算g，这个g称为激活函数

g(b1)=Y1  
g(b2)=Y2

ps: 方程求导后是常数的是线性方程，否则是非线性方程

非线性的激活函数

实际运用当中，有多种激活函数可以选择，这里我们介绍最经典的一种激活函数： sigmoid 激活函数，它的数学形式为：

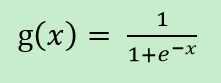
sigmoid 函数图像是

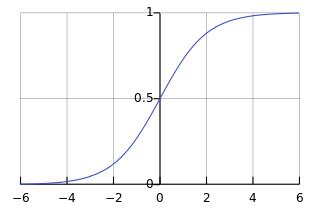
即输入值x越大，函数值越接近 1，输入值越小，函数值越接近 0，当输入为 0 的时候，函数值为 0.5。

上面是一个激活函数的例子，为什么使用非线性的激活函数呢？原因有几个：

多层网络的意义

• 深度神经网络是多层神经网络，如果没有非线性运算部分，由于 矩阵乘法的结合性，我们简算方程式后，多个线性运算层最终会简化成一个线性运算，多层次的网络结构失去了意义。

非线性分类更贴近实际

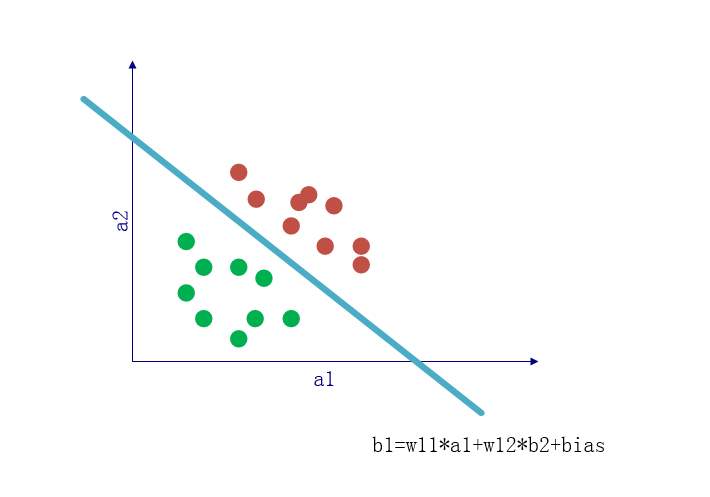
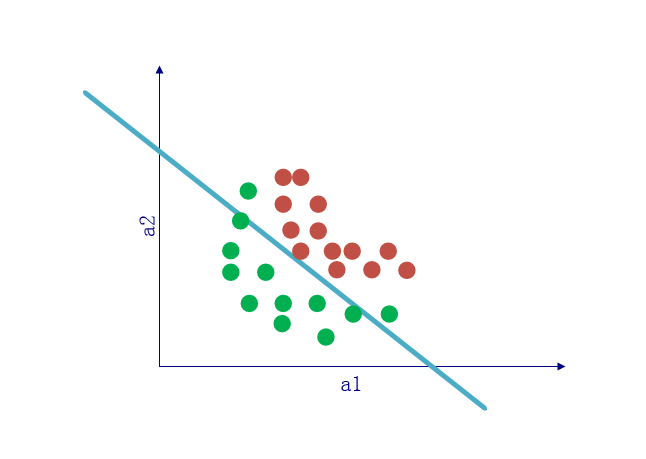
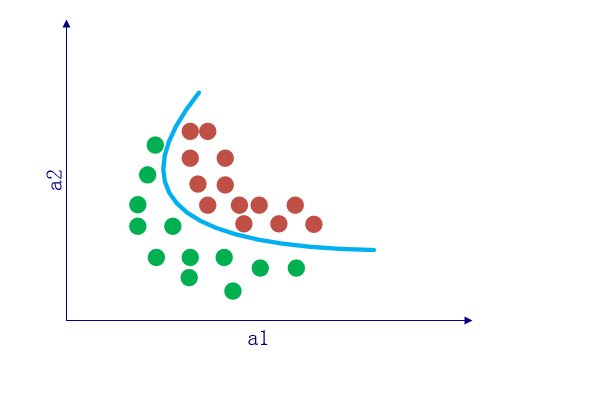
实际上，不同类别之间的分界线更多是曲线而不是直线，此时无论如何也无法用线性分类器去准确的进行分类。而非线性部分的引入，在一定程度上可以使原本的直线变成曲线。

当输入数据的维度为 3 时，单纯的线性运算就相当于是使用一个平面对空间进行划分，当数据维度高于 3 维时类似，只是我们已经无法直观的观察大于 3 维的空间了。

概率

非线性激活函数还有其他作用，比如sigmoid将输出值的范围限制在 0 到 1 之间，使其刚好可以被作为概率来看待。

评价神经网络的效果

如何设定神经网络中的网络参数值（包括连接线上的权重w和偏置值bias）。

• 一种最简单的方法是随机设定网络参数。如果神经网络中的网络参数是随机设置的，那么我们得到的 “网络性能” 应该就是随机情况下的平均值。比如我们要判断一些图片中的字母属于 26 个字母中的哪一个，如果网络参数值是随机设定的话，那我们得到的识别准确率理论上应该在 1/26 左右。随机设定参数值当然不可能是我们解决问题的办法。
• 如何设置 “好” 的网络参数值来使神经网络正确的工作，这是 网络性能 的问题。我们如何判定一个神经网络是 “好” 的还是 “不好” 的呢，即我们用什么来评价一个神经网络的效果呢？

损失函数

在有监督学习中，学习数据 data 包含输入数据的预期正确输出值，一个简单的办法是比较神经网络的输出 h 与预期的正确输出 y 之间的差异。比如计算(h-y)^2, 当得到的值比较大时，就说明我们的神经网络的输出与预期的正确输出偏差较大，反之，如果得到的值很小甚至等于 0，就说明我们的模型工作的不错，能够正确的预测输出值。

二次损失函数 quadratic loss

就像它的名字所暗示的那样，quadratic loss function 通过计算h和y之间差值的二次方，来表达一个神经网络的效果。具体形式如下：

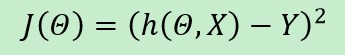
• 学习算法learn按照某种策略，通过不断的更新参数值来使损失函数 J(theta,X,Y) 的值减小，theta 是自变量。
• 上面公式J(theta,X,Y), 从训练算法的角度看，我们要训练的算法是 J(theta)，因为对于一个特定的问题来讲，输入 X 与输出 Y 可以视作常量。

梯度下降算法

衡量神经网络性能的办法:损失函数，训练算法是，就必须想办法让损失函数的值尽量小，最好是让损失函数值为0。

假设我们的损失函数图形是这样的：

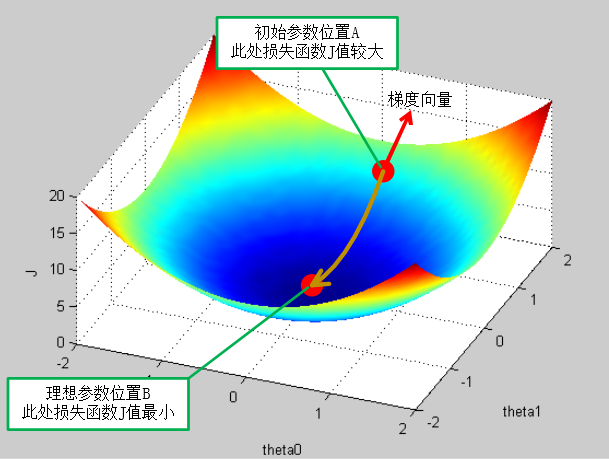
我们的目标是使A尽量靠近最低点B, 最好是与B重合，这样才能最小化损失函数。

梯度

梯度是一个向量，由损失函数对每个自变量（图中的 theta0 和 theta1）分别求偏导得到。

形象的理解，梯度指向损失函数变化最快的那个方向（且该方向让函数值变大），在图中的三维上，就是曲面上在 A 点最 “陡峭” 的方向。在二维上，是斜率方向。

梯度下降算法

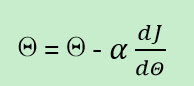
• 上图中，梯度的方向使损失函数的值变大，于是为了使 A 点向 B 点移动，就可以对 A 的值减去该点的梯度（alpha * 斜率）。
• 上面公式有一个希腊字母alpha，梯度表示更新参数 theta 的方向，而这个 alpha 表示往这个方向走多远。
• 当走到下一个位置之后，再求该点的梯度，用梯度更新参数位置，如此重复，直到逼近 B 点。这就是梯度下降算法的原理。
• alpha 在这里是一个 超参数（hyperparameter）

ps: 实际中，损失函数并不像图中的凸函数那么理想，梯度下降算法可能无法到达最低点，或者被“局部最低点”（梯度为0）欺骗而无法到达“全局最低点”。需要采取一些方法，暂不提。

参数 (parameter) 与超参数(hyper parameter)

模型 model 中的参数 theta 称为参数，而学习算法（即梯度下降算法）里的参数 alhpa 被称为超参数。它们区别在于：

• theta 被称为 “参数”，它决定了模型 model 的性质，最终值是由学习算法 learn 学习得到，不需要手工设定。
• alhpa 是学习算法 learn 中决定梯度下降算法每一步走多远的参数，它需要手工设定，决定了得到最优theta的过程。即超参数决定如何得到最优参数。

ps: 复杂问题的模型中可能有上亿个参数，这都由学习算法得到，而我们只需手动设置超参数。

超参数 alpha– 学习速率

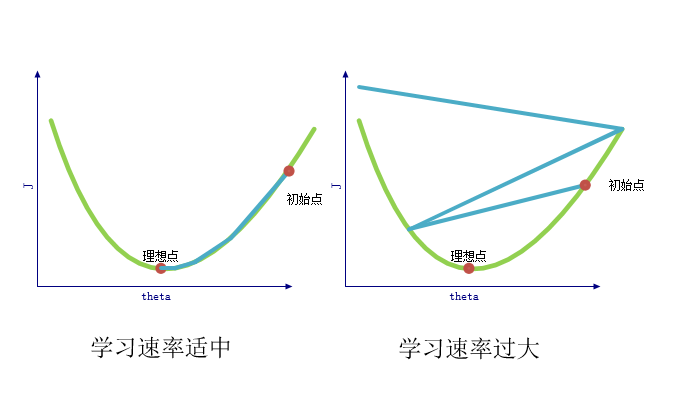
机器学习中，我们将上面提到的超参数alpha称为学习速率（learning rate）。这很好理解，因为alpha越大时，我们的参数theta更新的幅度越大，我们可能会更快的到达最低点。但是alpha不能设置的太大，否则有可能一次变化的太大导致 “步子太长”，会直接越过最低点，甚至导致损失函数值不降反升。

思考题

• “手工编程计算圆的面积”中，3.14 是 “参数” 还是“超参数”？

答：参数

• 一个如本次实验所描述的神经网络有两层，第一层有 10 个神经元，第二层有 20 个神经元，请问这两层神经元之间有多少条连接？第一层到第二层之间由这些连接所表示的线性变换矩阵尺寸是多少？

答：笛卡尓积，10*20=200 条连接。这些连接表示的矩阵，尺寸是：10列×20行

• “使用深度学习预测股票走势曲线” 是分类问题还是回归问题？

答：回归

• “根据人脸图片识别人的性别” 是分类问题还是回归问题？

答：分类

• 如果说，有监督学习的训练数据data由输入X和正确答案Y组成，那无监督学习的训练数据应该是什么样的？

答：-

• sigmoid 函数对 x 求导结果是什么？

答：

求导过程

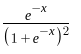
• “超参数 alpha– 学习速率” 小节中的图片里，为什么 “学习速率适中” 图中每次更新的 “步子” 越来越短，而 “学习速率过大” 图中每次更新的 “步子” 越来越长？

答：学习速率过大，导致梯度的斜率越来越 “陡峭”，越陡峭的斜率乘以过大的 alpha ，得到的 theta 偏移量越来越大。

• 你能自己想出一种求损失函数梯度的方法吗？

答：-